#install.packages(c("lavaan", "ggplot2", "Rfast", "MBESS", "future.apply"), dependencies = TRUE)
library("lavaan")
library("Rfast")
library("ggplot2")
library("dplyr")
library("MBESS")
library(future.apply)
# this initializes parallel processing, for faster code execution
# By default, it uses all available cores
plan(multisession)Ch. 5: Structural Equation Models
Reading/working time: ~50 min.
In this chapter, we will focus on some rather simple Structural Equation Models (SEM). The goal is to illustrate how simulations can be used to estimate statistical power to detect a given effect in a SEM. In the context of SEMs, the focal effect may be for instance a fit index (e.g., Chi-Square, Root Mean Square Error of Approximation, etc.) or a model coefficient (e.g., a regression coefficient for the association between two latent factors). In this chapter, we only focus on the latter, that is power analyses for regression coefficients in the context of SEM. Please see the bonus chapter titled “Power analysis for fit indices in SEM” if you’re interested in power analyses for fit indices.
Note
In this chapter, we’ll use the parallelization techniques described in the Chapter “Bonus: Optimizing R code for speed”, otherwise the simulations are too slow. If you wonder about the unknown commands in the code, please read the bonus chapter to learn how to considerably speed up your code! But nonetheless, running some of the chunks in this chapter will require quite some time. We therefore decided to use 500 iterations per simulation only in this chapter; please keep in mind that you should use more iterations in order to obtain more precise estimates!
A simulation-based power analysis for a single regression coefficient between latent variables
Let’s consider the following example: We are planning to conduct a study investigating whether people’s openness to experience (as conceptualized in the big five personality traits) relates negatively to generalized prejudice, that is a latent variable comprising prejudice towards different social groups (e.g., women, foreigners, homosexuals, disabled people). We could plan to scrutinize this prediction with a SEM in which both openness to experience and generalized prejudice are modeled as latent variables.
Note
Please note that the predictions used as examples in this chapter are not necessarily theoretically meaningful hypotheses, we merely use them to illustrate the mechanics of simulation-based power analyses in the context of SEM.
Let’s get some real data as starting point
Just like for any other simulation-based power analysis, we first need to come up with plausible estimates of the distribution of the (manifest) variables. For the sake of simplicity, let’s assume that there is a published study that measured manifestations of our two latent variables and that the corresponding data set is publicly available. For the purpose of this tutorial, we will draw on a publication by Bergh et al (2016) and the corresponding data set which has been made accessible as part of the MPsychoR package. Let’s take a look at this data set.
#install.packages("MPsychoR")
library(MPsychoR)
data("Bergh")
attach(Bergh)
#let's take a look
head(Bergh) EP SP HP DP A1 A2 A3 O1 O2 O3
1 2.666667 3.125 1.4 2.818182 3.4375 3.600000 3.352941 2.8750 3.400000 3.176471
2 2.666667 3.250 1.4 2.545455 2.3125 2.666667 3.117647 4.4375 3.866667 4.470588
3 1.000000 1.625 2.7 2.000000 3.5625 4.600000 3.941176 4.2500 3.666667 3.705882
4 2.666667 2.750 1.8 2.818182 2.7500 3.200000 3.352941 2.8750 3.400000 3.117647
5 2.888889 3.250 2.7 3.000000 3.2500 4.200000 3.764706 3.9375 4.400000 4.294118
6 2.000000 2.375 1.7 2.181818 3.2500 3.333333 2.941176 3.8125 3.066667 3.411765
gender
1 male
2 male
3 male
4 male
5 male
6 maletail(Bergh) EP SP HP DP A1 A2 A3 O1 O2
856 2.000000 2.500 1.0 2.363636 3.3125 3.800000 3.705882 3.6875 3.733333
857 1.555556 1.875 1.1 1.818182 2.6250 3.733333 3.000000 3.3125 2.800000
858 3.000000 2.750 1.0 1.909091 3.3125 3.533333 3.882353 4.0000 3.533333
859 1.444444 1.250 1.0 1.000000 3.8750 3.800000 3.529412 3.9375 3.533333
860 1.222222 1.625 1.0 2.363636 2.8750 3.600000 3.411765 2.8125 3.600000
861 1.555556 1.750 1.0 1.090909 3.3750 4.266667 4.058824 3.3750 2.800000
O3 gender
856 4.411765 female
857 3.529412 female
858 3.823529 female
859 3.411765 female
860 3.058824 female
861 3.588235 femaleThis data set comprises 11 variables measured in 861 participants. For now, we will focus on the following measured variables:
EPis a continuous variable measuring ethnic prejudice.SPis a continuous variable measuring sexism.HPis a continuous variable measuring sexual prejudice towards gays and lesbians.DPis a continuous variable measuring prejudice toward people with disabilities.O1,O2, andO3are three items measuring openness to experience.
To get an impression of this data, we look at the correlations of the variables we’re interested in.
cor(cbind(EP, SP, HP, DP, O1, O2, O3)) |> round(2) EP SP HP DP O1 O2 O3
EP 1.00 0.53 0.25 0.53 -0.35 -0.36 -0.41
SP 0.53 1.00 0.22 0.53 -0.33 -0.31 -0.33
HP 0.25 0.22 1.00 0.24 -0.23 -0.30 -0.29
DP 0.53 0.53 0.24 1.00 -0.30 -0.33 -0.34
O1 -0.35 -0.33 -0.23 -0.30 1.00 0.66 0.74
O2 -0.36 -0.31 -0.30 -0.33 0.66 1.00 0.71
O3 -0.41 -0.33 -0.29 -0.34 0.74 0.71 1.00As we have discussed in the previous chapters, the starting point of every simulation-based power analysis is to specify the population parameters of the variables of interest. In our example, we can estimate the population parameters from the study by Bergh et al. (2016). We start by calculating the means of the variables, rounding them generously, and storing them in a vector called means_vector.
#store means
means_vector <- c(mean(EP), mean(SP), mean(HP), mean(DP), mean(O1), mean(O2), mean(O3)) |> round(2)
#Let's take a look
means_vector[1] 1.99 2.11 1.22 2.06 3.55 3.49 3.61We also need the variance-covariance matrix of our variables in order to simulate data. Luckily, we can estimate this from the Bergh et al. data as well. There are two ways to do this. First, we can use the cov function to obtain the variance-covariance matrix. This matrix incorporates the variance of each variable on the diagonal, and the covariances in the remaining cells.
#store covariances
cov_mat <- cov(cbind(EP, SP, HP, DP, O1, O2, O3)) |> round(2)
#Let's take a look
cov_mat EP SP HP DP O1 O2 O3
EP 0.51 0.26 0.28 0.20 -0.12 -0.12 -0.15
SP 0.26 0.47 0.24 0.19 -0.11 -0.10 -0.12
HP 0.28 0.24 2.44 0.20 -0.18 -0.22 -0.23
DP 0.20 0.19 0.20 0.28 -0.08 -0.08 -0.09
O1 -0.12 -0.11 -0.18 -0.08 0.23 0.15 0.18
O2 -0.12 -0.10 -0.22 -0.08 0.15 0.22 0.17
O3 -0.15 -0.12 -0.23 -0.09 0.18 0.17 0.26This works well as long as we have a data set (e.g., from a pilot study or published work) to estimate the variances and covariances. In other cases, however, we might not have access to such a data set. In this case, we might only have a correlation table that was provided in a published paper. But that’s no problem either, as we can transform the correlations and standard deviations of the variables of interest into a variance-covariance matrix. The following chunk shows how this works by using the cor2cov function from the MBESS package.
#store correlation matrix
cor_mat <- cor(cbind(EP, SP, HP, DP, O1, O2, O3))
#store standard deviations
sd_vector <- c(sd(EP), sd(SP), sd(HP), sd(DP), sd(O1), sd(O2), sd(O3))
#transform correlations and standard deviations into variance-covariance matrix
cov_mat2 <- MBESS::cor2cov(cor.mat = cor_mat, sd = sd_vector) |> as.data.frame() |> round(2)
#Let's take a look
cov_mat2 EP SP HP DP O1 O2 O3
EP 0.51 0.26 0.28 0.20 -0.12 -0.12 -0.15
SP 0.26 0.47 0.24 0.19 -0.11 -0.10 -0.12
HP 0.28 0.24 2.44 0.20 -0.18 -0.22 -0.23
DP 0.20 0.19 0.20 0.28 -0.08 -0.08 -0.09
O1 -0.12 -0.11 -0.18 -0.08 0.23 0.15 0.18
O2 -0.12 -0.10 -0.22 -0.08 0.15 0.22 0.17
O3 -0.15 -0.12 -0.23 -0.09 0.18 0.17 0.26Let’s do a plausibility check: Did the two ways to estimate the variance-covariance matrix lead to the same results?
cov_mat == cov_mat2 EP SP HP DP O1 O2 O3
EP TRUE TRUE TRUE TRUE TRUE TRUE TRUE
SP TRUE TRUE TRUE TRUE TRUE TRUE TRUE
HP TRUE TRUE TRUE TRUE TRUE TRUE TRUE
DP TRUE TRUE TRUE TRUE TRUE TRUE TRUE
O1 TRUE TRUE TRUE TRUE TRUE TRUE TRUE
O2 TRUE TRUE TRUE TRUE TRUE TRUE TRUE
O3 TRUE TRUE TRUE TRUE TRUE TRUE TRUEIndeed, this worked! Both procedures lead to the exact same variance-covariance matrix. Now that we have an approximation of the variance-covariance matrix, we use the rmvnorm function from the Rfast package to simulate data from a multivariate normal distribution. The following code simulates n = 50 observations from the specified population.
#Set seed to make results reproducible
set.seed(21364)
#simulate data
my_first_simulated_data <- Rfast::rmvnorm(n = 50, mu=means_vector, sigma = cov_mat) |> as.data.frame()
#Let's take a look
head(my_first_simulated_data) EP SP HP DP O1 O2 O3
1 1.175231 2.1563276 -0.4498951 1.535653 3.520299 3.768441 3.877645
2 2.615520 1.7527931 -0.2546117 1.728349 3.048912 2.816513 2.743648
3 1.849380 2.0383562 -0.3877381 2.055153 3.516697 3.354251 3.792305
4 1.901085 2.5438523 2.0475777 2.150921 3.824178 3.631459 3.947051
5 2.182503 2.1326429 -0.2088395 2.674773 3.948864 3.642066 4.005110
6 1.691124 0.9746677 1.9193559 1.652397 4.184485 3.236144 3.669261We could now fit a SEM to this simulated data set and check whether the regression coefficient modelling the association between openness to experience and generalized prejudice is significant at an \alpha-level of .005. We will work with the lavaan package to fit SEMs.
#specify SEM
model_sem <- "generalized_prejudice =~ EP + DP + SP + HP
openness =~ O1 + O2 + O3
generalized_prejudice ~ openness"
#fit the SEM to the simulated data set
fit_sem <- sem(model_sem, data = my_first_simulated_data)
#display the results
summary(fit_sem)lavaan 0.6.15 ended normally after 36 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 15
Number of observations 50
Model Test User Model:
Test statistic 20.528
Degrees of freedom 13
P-value (Chi-square) 0.083
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|)
generalized_prejudice =~
EP 1.000
DP 0.891 0.298 2.989 0.003
SP 1.156 0.383 3.022 0.003
HP 0.321 0.677 0.474 0.636
openness =~
O1 1.000
O2 0.857 0.155 5.544 0.000
O3 1.370 0.225 6.086 0.000
Regressions:
Estimate Std.Err z-value P(>|z|)
generalized_prejudice ~
openness -0.259 0.204 -1.270 0.204
Variances:
Estimate Std.Err z-value P(>|z|)
.EP 0.352 0.082 4.277 0.000
.DP 0.084 0.037 2.292 0.022
.SP 0.165 0.064 2.577 0.010
.HP 2.475 0.496 4.990 0.000
.O1 0.065 0.019 3.433 0.001
.O2 0.067 0.017 3.996 0.000
.O3 0.045 0.027 1.655 0.098
.generlzd_prjdc 0.138 0.078 1.766 0.077
openness 0.116 0.036 3.182 0.001The results show that in this case, the regression coefficient is -0.26 which is significant with p = 0.204. But, actually, it is not our primary interest to see whether this particular simulated data set results in a significant regression coefficient. Rather, we want to know how many of a theoretically infinite number of simulations yield a significant p-value of the focal regression coefficient. Thus, as in the previous chapters, we now repeatedly simulate data sets of a certain size (say, 50 observations) from the specified population and store the results of the focal test (here: the p-value of the regression coefficient) in a vector called p_values.
#Set seed to make results reproducible
set.seed(21364)
#let's do 500 iterations
iterations <- 500
#prepare an empty NA vector with 500 slots
p_values <- rep(NA, iterations)
#sample size per iteration
n <- 50
#simulate data
for(i in 1:iterations){
simulated_data <- Rfast::rmvnorm(n = n, mu = means_vector, sigma = cov_mat) |> as.data.frame()
fit_sem_simulated <- sem(model_sem, data = simulated_data)
p_values[i] <- parameterestimates(fit_sem_simulated)[8,]$pvalue
}How many of our 500 virtual samples would have found a significant p-value (i.e., p < .005)?
#frequency table
table(p_values < .005)
FALSE TRUE
144 356 #percentage of significant results
sum(p_values < .005)/iterations*100[1] 71.2Only 71.2% of samples with the same size of n=50 result in a significant p-value. We conclude that n=50 observations seems to be insufficient, as the power with these parameters is lower than 80%.
Sample size planning: Find the necessary sample size
But how many observations do we need to find the presumed effect with a power of 80%? Like before, we can now systematically vary certain parameters (e.g., sample size) of our simulation and see how that affects power. We could, for example, vary the sample size in a range from 30 to 200. Running these simulations typically requires quite some computing time.
#Set seed to make results reproducible
set.seed(21364)
#test ns between 30 and 200
ns_sem <- seq(30, 200, by=10)
#prepare empty vector to store results
result_sem <- data.frame()
#set number of iterations
iterations_sem <- 500
#write function
sim_sem <- function(n, model, mu, sigma) {
simulated_data <- Rfast::rmvnorm(n = n, mu = mu, sigma = sigma) |> as.data.frame()
fit_sem_simulated <- sem(model, data = simulated_data)
p_value_sem <- parameterestimates(fit_sem_simulated)[8,]$pvalue
return(p_value_sem)
}
#replicate function with varying ns
for (n in ns_sem) {
p_values_sem <- future_replicate(iterations_sem, sim_sem(n = n, model = model_sem, mu = means_vector, sigma = cov_mat), future.seed=TRUE)
result_sem <- rbind(result_sem, data.frame(
n = n,
power = sum(p_values_sem < .005)/iterations_sem)
)
#The following line of code can be used to track the progress of the simulations
#This can be helpful for simulations with a high number of iterations and/or a large parameter space which require a lot of time
#I have deactivated this here; to enable it, just remove the "#" sign at the beginning of the next line
#message(paste("Progress info: Simulations completed for n =", n))
}Let’s plot the results:
ggplot(result_sem, aes(x=n, y=power)) + geom_point() + geom_line() + scale_x_continuous(n.breaks = 18, limits = c(30,200)) + scale_y_continuous(n.breaks = 10, limits = c(0,1)) + geom_hline(yintercept= 0.8, color = "red")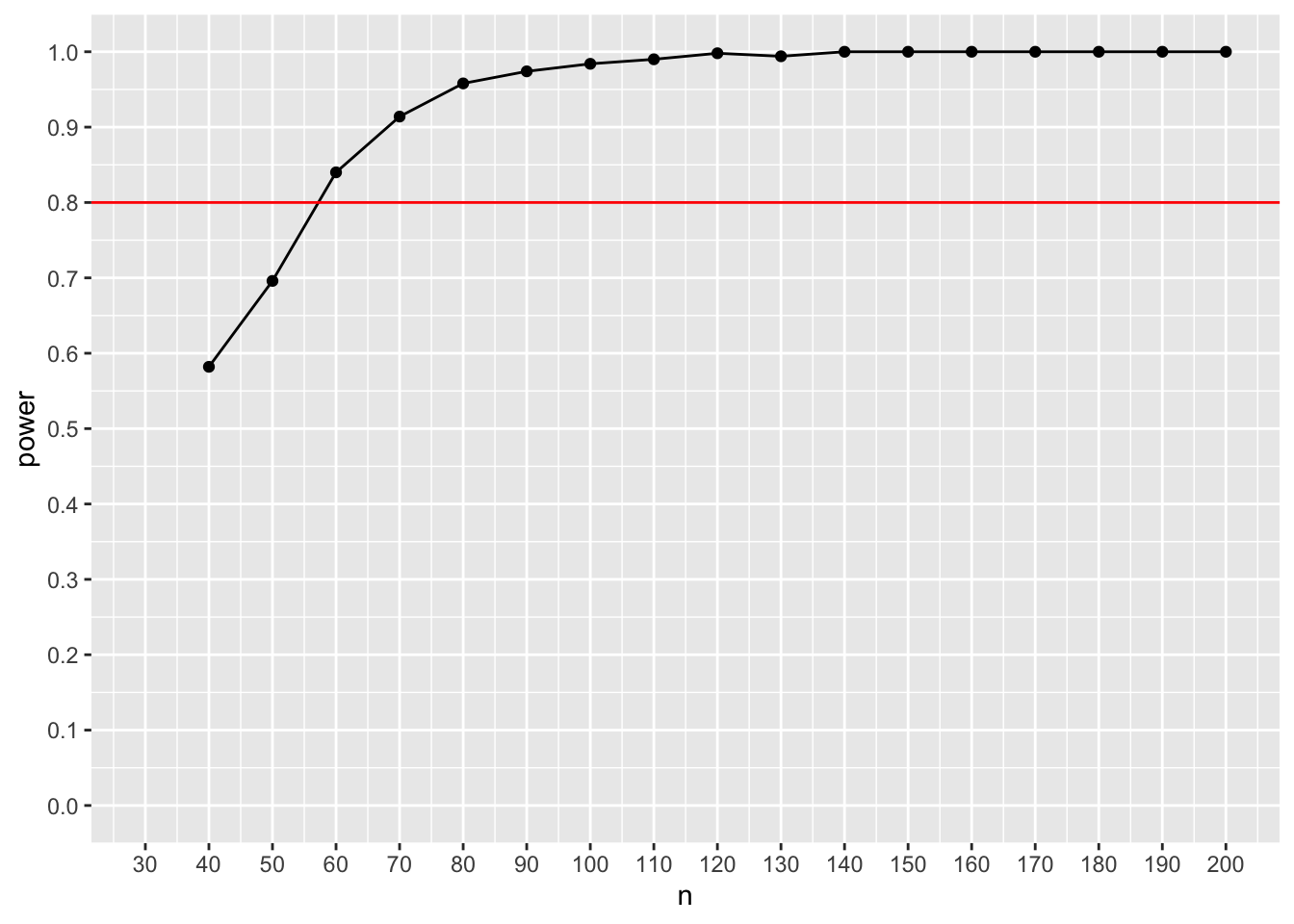
This graph suggests that we need a sample size of approximately 50 participants to reach a power of 80% with the given population estimates. That’s all it takes to run a power analysis for a SEM!
In the following two sub-paragraphs, we would like to present two alternatives and/or extensions to this first way of doing a power analysis for a SEM. First, we would like to present an alternative way to simulate data for SEMs, i.e. by using a built-in function in the lavaan package. Second, we would like to show how a “safeguard” approach to power analysis can be used within the context of SEM.
Using the lavaan syntax to simulate data
In our opening example in this chapter, we used the rmvnorm function from the Rfastpackage to simulate data based on the means of the manifest variables as well as their variance-covariance matrix. An alternative to this procedure is to use a built-in function in the lavaan package, that is, the simulateData() function. The main idea here is to provide this function with a lavaan model that specifies all relevant population parameters and then to use this function to directly simulate data.
More specifically, we need to incorporate the factor loadings, regression coefficients and (residual) variances of all latent and manifest variables in the lavaan syntax. As these parameters are hardly ever known without a previous study, we will again draw on the results from the data by Bergh et al (2016). Let’s again take a look at the results of our SEM when applying it to this data set.
#fit the SEM to the pilot data set
fit_bergh <- sem(model_sem, data = Bergh)
#display the results
summary(fit_bergh)lavaan 0.6.15 ended normally after 40 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 15
Number of observations 861
Model Test User Model:
Test statistic 40.574
Degrees of freedom 13
P-value (Chi-square) 0.000
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|)
generalized_prejudice =~
EP 1.000
DP 0.710 0.041 17.383 0.000
SP 0.907 0.052 17.337 0.000
HP 1.042 0.112 9.267 0.000
openness =~
O1 1.000
O2 0.932 0.035 26.255 0.000
O3 1.143 0.040 28.923 0.000
Regressions:
Estimate Std.Err z-value P(>|z|)
generalized_prejudice ~
openness -0.766 0.056 -13.641 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.EP 0.219 0.016 13.403 0.000
.DP 0.141 0.009 14.972 0.000
.SP 0.233 0.015 15.079 0.000
.HP 2.124 0.106 19.965 0.000
.O1 0.073 0.005 14.423 0.000
.O2 0.079 0.005 15.805 0.000
.O3 0.052 0.005 9.823 0.000
.generlzd_prjdc 0.191 0.018 10.362 0.000
openness 0.161 0.011 14.210 0.000In order to use the simulateData() function, we can take the estimates from this previous study and plug them into the lavaan syntax in the following chunk.
#Set seed to make results reproducible
set.seed(21364)
#specify SEM
model_fully_specified <-
"generalized_prejudice =~ 1*EP + 0.71*DP + 0.91*SP + 1*HP
openness =~ 1*O1 + 0.93*O2 + 1.14*O3
generalized_prejudice ~ -0.77*openness
generalized_prejudice ~~ 0.19*generalized_prejudice
openness ~~ 0.16*openness
EP ~~ 0.21*EP
DP ~~ 0.14*DP
SP ~~ 0.23*SP
HP ~~ 2.12*HP
O1 ~~ 0.07*O1
O2 ~~ 0.08*O2
O3 ~~ 0.05*O3
"
#lets try this
sim_lavaan <- simulateData(model_fully_specified, sample.nobs=100)
head(sim_lavaan) EP DP SP HP O1 O2
1 0.009175975 -0.4818076 -0.29785829 -3.5273250 -0.02254289 -0.1394437
2 -0.204483904 -0.4787598 0.15013918 -3.1894504 -0.56917823 -0.2076622
3 0.456774325 -0.6544974 0.05802164 -2.3337546 0.26092341 0.7767911
4 -1.153264826 -0.3216415 -0.91603659 -2.0334785 -0.16649019 -0.1387532
5 0.512683482 0.3138148 0.28465681 0.1202821 -0.41602783 -0.2699893
6 -1.064347791 -0.3287166 -0.62215235 -2.4007914 0.60927732 -0.1814121
O3
1 -0.22583796
2 -1.17504320
3 0.11402119
4 0.06726909
5 -0.62531893
6 0.13393737The next step is to integrate this code into our first simulation-based power analysis in this chapter, that is, to replace the data simulation process using the rmvnorm function from the Rfast package with this new method using simulateData() from the lavaan package. To this end, I am adapting the power analysis SEM chunk from above accordingly.
#Set seed to make results reproducible
set.seed(21364)
#test ns between 30 and 200
ns_sem <- seq(30, 200, by=10)
#prepare empty vector to store results
result_sem <- data.frame()
#set number of iterations
iterations_sem <- 500
#write function
sim_sem_lavaan <- function(n, model) {
sim_lavaan <- simulateData(model = model, sample.nobs=n)
fit_sem_simulated <- sem(model_sem, data = sim_lavaan)
p_value_sem <- parameterestimates(fit_sem_simulated)[8,]$pvalue
return(p_value_sem)
}
#replicate function with varying ns
for (n in ns_sem) {
p_values_sem <- future_replicate(iterations_sem, sim_sem_lavaan(n = n, model = model_fully_specified), future.seed=TRUE)
result_sem <- rbind(result_sem, data.frame(
n = n,
power = sum(p_values_sem < .005, na.rm = TRUE)/iterations_sem)
)
#The following line of code can be used to track the progress of the simulations
#This can be helpful for simulations with a high number of iterations and/or a large parameter space which require a lot of time
#I have deactivated this here; to enable it, just remove the "#" sign at the beginning of the next line
#message(paste("Progress info: Simulations completed for n =", n))
}Let’s plot this again.
ggplot(result_sem, aes(x=n, y=power)) + geom_point() + geom_line() + scale_x_continuous(n.breaks = 18, limits = c(30,200)) + scale_y_continuous(n.breaks = 10, limits = c(0,1)) + geom_hline(yintercept= 0.8, color = "red")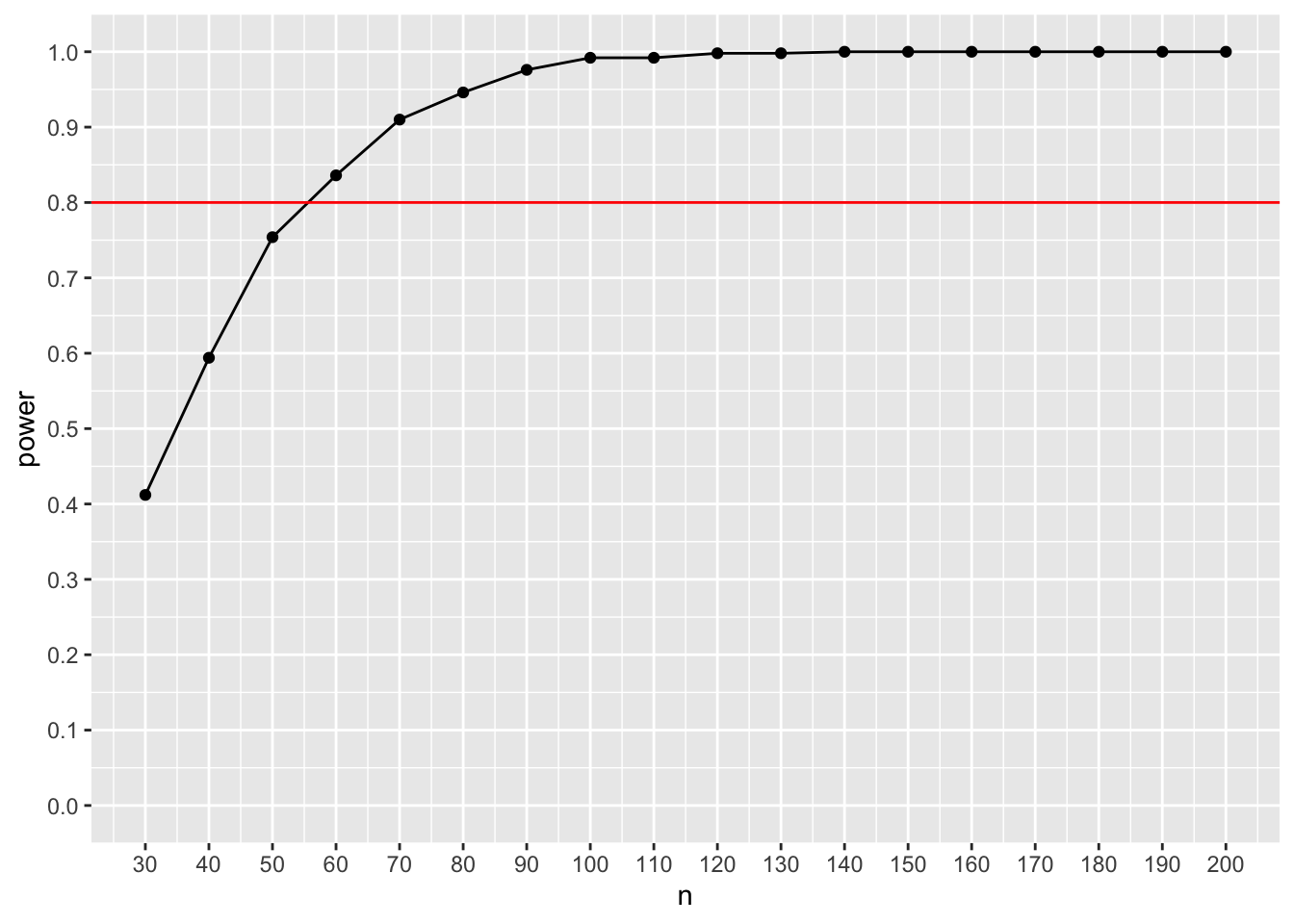
Here, we conclude that approx. 55 participants would be needed to achieve 80% power. The slight difference compared to the previous power analysis should be explained by the fact that we rounded the numbers that define our statistical populations and that we only used 500 Monte Carlo iterations – these differences should decrease with an increasing number of iterations.
Tip
Wang and Rhemtulla (2021) developed a shiny app that can do power analyses for SEMs in a similar fashion, but that additionally provides a point-and-click interface. You can use it here, for instance, to replicate the results of this simulation-based power analysis: https://yilinandrewang.shinyapps.io/pwrSEM/
A safeguard power approach for SEMs
Of note, the two power analyses for our SEM we have conducted so far used the observed effect size from the Bergh et al. (2016) data set as an estimate of the “true” effect size. But, as this point estimate may be imprecise (e.g., because of publication bias), it seems reasonable to use a more conservative estimate of the true effect size. One more conservative approach in this context is the safeguard power approach (Perugini et al., 2014), which we have already applied in Chapter 1 (Linear Model I: a single dichotomous predictor).
Basically, all need to do in order to account for variability of observed effect sizes is to calculate a 60%-confidence interval around the point estimate of the observed effect size from our pilot data and to use the more conservative bound of this confidence interval (here: the upper bound) as our new effect size estimate. This can be easily done with the parameterestimates function from the lavaan package which takes the level of the confidence interval as an input parameter. Let’s use this function on our object fit_bergh which stores the results of our SEM in the Bergh data set.
parameterestimates(fit_bergh, level = .60) lhs op rhs est se z pvalue
1 generalized_prejudice =~ EP 1.000 0.000 NA NA
2 generalized_prejudice =~ DP 0.710 0.041 17.383 0
3 generalized_prejudice =~ SP 0.907 0.052 17.337 0
4 generalized_prejudice =~ HP 1.042 0.112 9.267 0
5 openness =~ O1 1.000 0.000 NA NA
6 openness =~ O2 0.932 0.035 26.255 0
7 openness =~ O3 1.143 0.040 28.923 0
8 generalized_prejudice ~ openness -0.766 0.056 -13.641 0
9 EP ~~ EP 0.219 0.016 13.403 0
10 DP ~~ DP 0.141 0.009 14.972 0
11 SP ~~ SP 0.233 0.015 15.079 0
12 HP ~~ HP 2.124 0.106 19.965 0
13 O1 ~~ O1 0.073 0.005 14.423 0
14 O2 ~~ O2 0.079 0.005 15.805 0
15 O3 ~~ O3 0.052 0.005 9.823 0
16 generalized_prejudice ~~ generalized_prejudice 0.191 0.018 10.362 0
17 openness ~~ openness 0.161 0.011 14.210 0
ci.lower ci.upper
1 1.000 1.000
2 0.676 0.744
3 0.863 0.951
4 0.948 1.137
5 1.000 1.000
6 0.902 0.962
7 1.110 1.176
8 -0.814 -0.719
9 0.205 0.233
10 0.133 0.148
11 0.220 0.246
12 2.034 2.213
13 0.069 0.078
14 0.074 0.083
15 0.048 0.057
16 0.175 0.206
17 0.152 0.171This output shows that the upper bound of the 60% confidence interval around the focal regression coefficient is -0.72. We can now use this as our new and more conservative effect size estimate. We can for example insert this value into our simulation using the lavaan syntax. For this purpose, we copy the chunk from above and simply replace the previous effect size estimate (-0.77) with the new estimate (-0.72), while keeping all other parameters that define this data set.
#Set seed to make results reproducible
set.seed(21364)
#specify SEM
model_fully_specified_safeguard <-
"generalized_prejudice =~ 1*EP + 0.71*DP + 0.91*SP + 1*HP
openness =~ 1*O1 + 0.93*O2 + 1.14*O3
generalized_prejudice ~ -0.72*openness
generalized_prejudice ~~ 0.19*generalized_prejudice
openness ~~ 0.16*openness
EP ~~ 0.21*EP
DP ~~ 0.14*DP
SP ~~ 0.23*SP
HP ~~ 2.12*HP
O1 ~~ 0.07*O1
O2 ~~ 0.08*O2
O3 ~~ 0.05*O3
"
#lets try this
sim_lavaan_safeguard <- simulateData(model_fully_specified_safeguard, sample.nobs=100)
head(sim_lavaan_safeguard) EP DP SP HP O1 O2
1 0.03163582 -0.4674398 -0.2762416 -3.5075535 -0.04391145 -0.1593227
2 -0.19674199 -0.4764434 0.1605740 -3.1573002 -0.58997086 -0.2268869
3 0.48315832 -0.6351419 0.0799879 -2.3272372 0.25229795 0.7683784
4 -1.13893054 -0.3131634 -0.9001980 -2.0386232 -0.18372798 -0.1543441
5 0.49985196 0.3039113 0.2740270 0.1386227 -0.41638579 -0.2703941
6 -1.04098556 -0.3130325 -0.5996895 -2.4067345 0.59293247 -0.1965773
O3
1 -0.25024294
2 -1.19986667
3 0.10431698
4 0.04700113
5 -0.62587386
6 0.11528181Now, everything is ready for the actual safeguard power analysis. We can re-use the sim_sem_lavaan function we have defined above. Let’s see what we get here!
#Set seed to make results reproducible
set.seed(21364)
#prepare empty vector to store results
result_sem_safeguard <- data.frame()
#replicate function with varying ns
for (n in ns_sem) {
p_values_sem_safeguard <- future_replicate(iterations_sem, sim_sem_lavaan(n = n, model = model_fully_specified_safeguard), future.seed=TRUE)
result_sem_safeguard <- rbind(result_sem_safeguard, data.frame(
n = n,
power = sum(p_values_sem_safeguard < .005, na.rm = TRUE)/iterations_sem)
)
#The following line of code can be used to track the progress of the simulations
#This can be helpful for simulations with a high number of iterations and/or a large parameter space which require a lot of time
#I have deactivated this here; to enable it, just remove the "#" sign at the beginning of the next line
#message(paste("Progress info: Simulations completed for n =", n))
}
ggplot(result_sem_safeguard, aes(x=n, y=power)) + geom_point() + geom_line() + scale_x_continuous(n.breaks = 18, limits = c(30,200)) + scale_y_continuous(n.breaks = 10, limits = c(0,1)) + geom_hline(yintercept= 0.8, color = "red")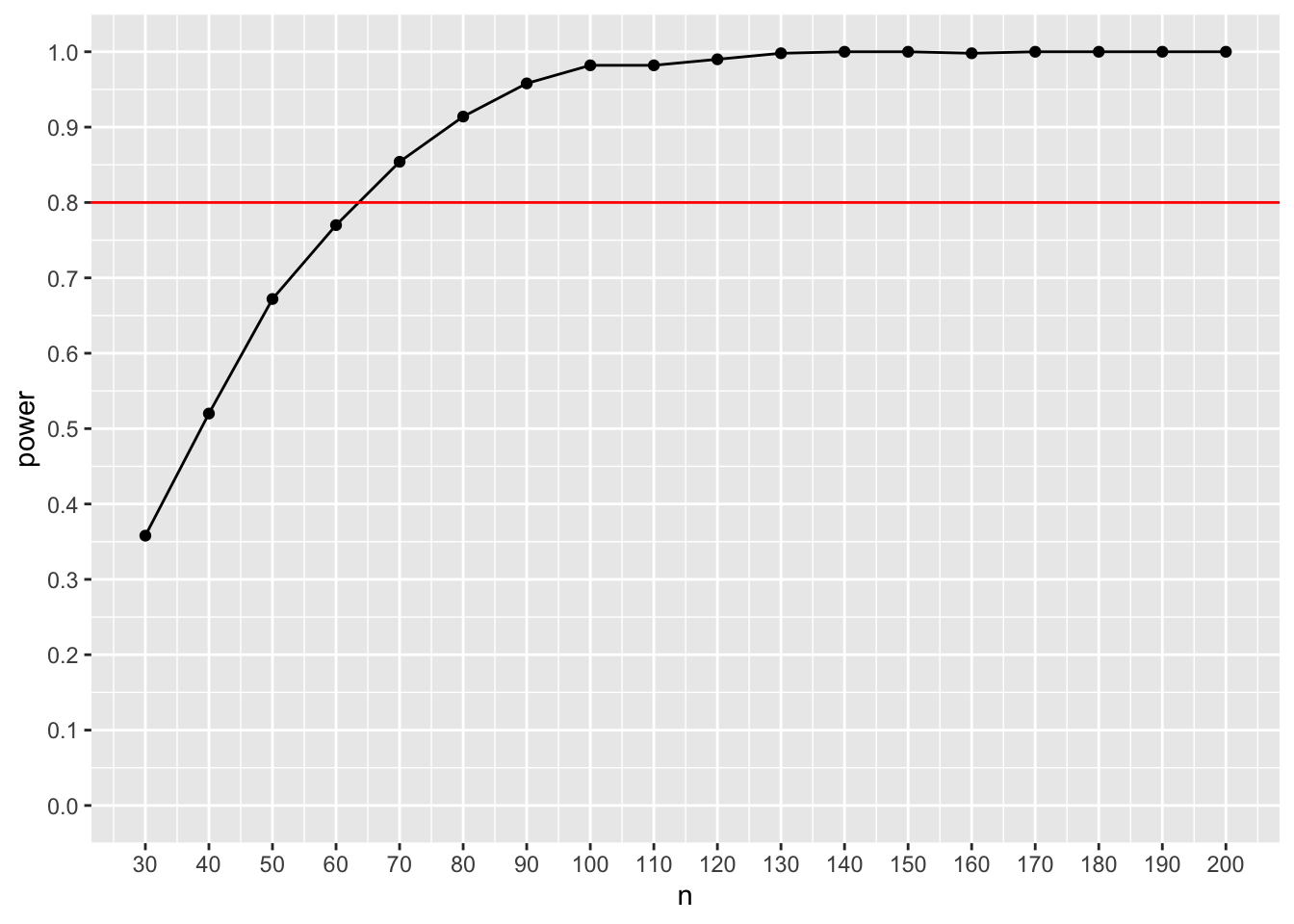
This safeguard power analysis yields a required sample size of ca. 63 participants.
Note
In addition to this safeguard power approach, we would also have liked to derive a smallest effect size of interest (SESOI). However, no prior studies on SESOI in the context of personality/stereotypes were available and the measures/response scales used by Bergh et al (2016) were only vaguely reported in their manuscript, thereby making it difficult to derive a meaningful SESOI. We therefore only report a safeguard approach but no SESOI approach here.
A simulation-based power analysis for a mediation model with latent variables
Sometimes, researchers not only wish to investigate whether and how two (latent) variables related to each other, but also whether the association between two (manifest or latent) variables is mediated by a third variable. We will run a power analysis for such a latent mediation model, investigating whether gender affects generalized prejudice (fully or partially) through openness to experience, while using the Bergh et al (2016) dataset as a pilot study. We can repeat the same steps as in our previous power analysis, while incorporating gender into our analysis. Specifically, we will follow these steps:
- find plausible estimates of the population parameters
- specify the statistical model
- simulate data from this population
- compute the index of interest (e.g., the p-value) and store the results
- repeat steps 2) and 3) multiple times
- count how many samples would have detected the specified effect (i.e., compute the statistical power)
- vary your simulation parameters until the desired level of power (e.g., 80%) is achieved
We first draw on the Bergh et al (2016) data set to estimate the means and the variance-covariance matrix. In this data set, gender is a factor with two levels, male and female. We first need to transform this categorical variable into an integer variable, for instance coding male = 0 and female = 1.
Bergh_int <- Bergh
Bergh_int$gender <- ifelse(Bergh_int$gender == "male", 0, ifelse(Bergh_int$gender == "female", 1, NA))
attach(Bergh_int)Die folgenden Objekte sind maskiert von Bergh:
A1, A2, A3, DP, EP, gender, HP, O1, O2, O3, SP#store means
means_mediation <- c(mean(gender), mean(EP), mean(SP), mean(HP), mean(DP), mean(O1), mean(O2), mean(O3)) |> round(2)
#store covarainces
cov_mediation <- cov(cbind(gender, EP, SP, HP, DP, O1, O2, O3)) |> round(2)
Tip
If we were interested in a mediation model with only manifest variables, we could also use a useful shiny app developed by Schoemann et al. (2017), which can be accessed via https://schoemanna.shinyapps.io/mc_power_med/. This app currently enables power analyses for some manifest mediation models: Mediation with (i) one mediator, (ii) two parallel mediators, (iii) two serial mediators, (iv) and three parallel mediators. But as we want to incorporate generalized prejudice and openness to experience as latent variables, we need to write a simulation-based power analyses ourselves.
Now, we specify the statistical mediation model in lavaan.
#specify mediation model
model_mediation <- '
# measurement model
generalized_prejudice =~ EP + DP + SP + HP
openness =~ O1 + O2 + O3
# direct effect
generalized_prejudice ~ c*gender
# mediator
openness ~ a*gender
generalized_prejudice ~ b*openness
# indirect effect (a*b)
ab := a*b
# total effect
total := c + (a*b)
'To verify that this model syntax works properly, we can fit this model to the data set provided by Bergh et al. (2016).
#fit the SEM to the simulated data set
fit_mediation <- sem(model_mediation, data = Bergh_int)
#display the results
summary(fit_mediation)lavaan 0.6.15 ended normally after 39 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 17
Number of observations 861
Model Test User Model:
Test statistic 84.622
Degrees of freedom 18
P-value (Chi-square) 0.000
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|)
generalized_prejudice =~
EP 1.000
DP 0.723 0.042 17.332 0.000
SP 0.962 0.054 17.722 0.000
HP 1.057 0.115 9.174 0.000
openness =~
O1 1.000
O2 0.931 0.035 26.266 0.000
O3 1.142 0.039 28.923 0.000
Regressions:
Estimate Std.Err z-value P(>|z|)
generalized_prejudice ~
gender (c) -0.268 0.039 -6.815 0.000
openness ~
gender (a) 0.094 0.032 2.950 0.003
generalized_prejudice ~
openness (b) -0.712 0.054 -13.245 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.EP 0.233 0.016 14.383 0.000
.DP 0.142 0.009 15.316 0.000
.SP 0.217 0.015 14.405 0.000
.HP 2.130 0.106 20.005 0.000
.O1 0.073 0.005 14.395 0.000
.O2 0.079 0.005 15.798 0.000
.O3 0.052 0.005 9.855 0.000
.generlzd_prjdc 0.168 0.017 10.051 0.000
.openness 0.160 0.011 14.210 0.000
Defined Parameters:
Estimate Std.Err z-value P(>|z|)
ab -0.067 0.023 -2.891 0.004
total -0.335 0.044 -7.552 0.000Now, everything is set up to run the actual power analysis. In the following chunk, we repeatedly simulate data from the specified population and store the p-value of the indirect effect while varying the sample size in a range from 500 to 1500.
#Set seed to make results reproducible
set.seed(21364)
#test ns between 100 and 1500
ns_mediation <- seq(500, 1500, by=50)
#prepare empty vector to store results
result_mediation <- data.frame()
#iterations
iterations_mediation <- 500
#write function
sim_mediation <- function(n, model, mu, sigma) {
simulated_data_mediation <- Rfast::rmvnorm(n = n, mu = mu, sigma = sigma) |> as.data.frame()
fit_mediation_simulated <- sem(model, data = simulated_data_mediation)
p_value_mediation <- parameterestimates(fit_mediation_simulated)[21,]$pvalue
return(p_value_mediation)
}
#replicate function with varying ns
for (n in ns_mediation) {
p_values_mediation <- future_replicate(iterations_mediation, sim_mediation(n = n, model = model_mediation, mu = means_mediation, sigma = cov_mediation), future.seed=TRUE)
result_mediation <- rbind(result_mediation, data.frame(
n = n,
power = sum(p_values_mediation < .005)/iterations_mediation)
)
#The following line of code can be used to track the progress of the simulations
#This can be helpful for simulations with a high number of iterations and/or a large parameter space which require a lot of time
#I have deactivated this here; to enable it, just remove the "#" sign at the beginning of the next line
#message(paste("Progress info: Simulations completed for n =", n))
}Let’s plot the results:
ggplot(result_mediation, aes(x=n, y=power)) + geom_point() + geom_line() + scale_y_continuous(n.breaks = 10) + scale_x_continuous(n.breaks = 20) + geom_hline(yintercept= 0.8, color = "red")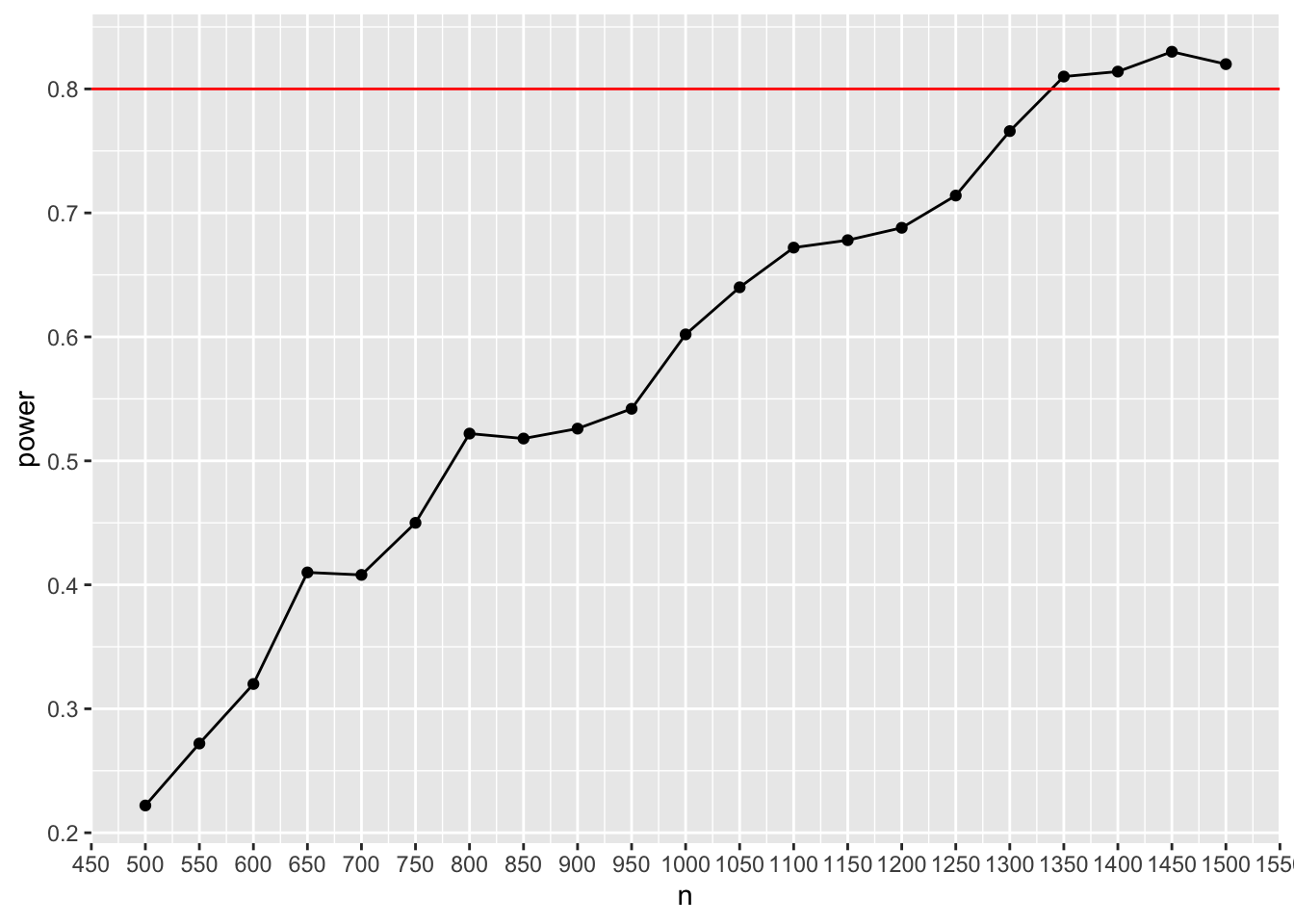
This shows that roughly 1,300 to 1,400 participants will be needed to obtain sufficient power under the assumptions we specified. To achieve a more precise estimate, just increase the number of iterations (and get a cup of coffee while you wait for the results 😅)
References
Bergh, R., Akrami, N., Sidanius, J., & Sibley, C. G. (2016). Is group membership necessary for understanding generalized prejudice? A re-evaluation of why prejudices are interrelated. Journal of Personality and Social Psychology, 111(3), 367–395. https://doi.org/10.1037/pspi0000064
Perugini, M., Gallucci, M., & Costantini, G. (2014). Safeguard power as a protection against imprecise power estimates. Perspectives on Psychological Science, 9(3), 319–332. https://doi.org/10.1177/1745691614528519
Schoemann, A. M., Boulton, A. J., & Short, S. D. (2017). Determining power and sample size for simple and complex mediation models. Social Psychological and Personality Science, 8(4), 379–386. https://doi.org/10.1177/1948550617715068
Wang, Y. A., & Rhemtulla, M. (2021). Power analysis for parameter estimation in structural equation modeling: A discussion and tutorial. Advances in Methods and Practices in Psychological Science, 4(1), 1–17. https://doi.org/10.1177/2515245920918253